Você já aprendeu em postagens anteriores a calcular a área de um círculo, assim como outras figuras planas, como os triângulos e quadriláteros. A seguir, vamos aprender a calcular áreas circulares, que são: a coroa circular, o setor circular e o segmento circular. Utilizaremos o conhecimento já adquirido para proporcionar um melhor aproveitamento do conteúdo!
Antes de mais nada vamos relembrar a área do círculo. Um circulo qualquer de raio r possui área igual a:
![]()
A dimensão, no sistema internacional de medidas é o metro quadrado (m²), e fora isso outras unidades usuais, como os milímetros quadrados (mm²) ou centímetros quadrados (cm²), entres outras unidades.
Feito isso, começaremos explicando sobre a coroa circular. Uma coroa circular é obtida através da sobreposição de dois círculos, os quais devem estar concêntricos, ou seja, o centro de ambos deve ser o mesmo! Além disso, obviamente, as circunferências devem ter diâmetros diferentes, de modo a criar uma coroa, que é a diferença entre as áreas da circunferência maior, de raio R, e da circunferência menor, com raio igual a r. Veja abaixo uma representação da coroa circular:

Equacionando a área da coroa circular, temos que:

Desta forma, quanto maior a diferença entre os raios, maior será a área da coroa calculada!
Outra área circular que podemos determinar é a área de uma seção circular. Quando falamos de um círculo completo, estamos falando de uma figura com 360º. No entanto, em diversas situações, não temos um círculo completo, mas sim apenas uma parcela deste. Por exemplo, ao comprar uma pizza dividida em oito pedaços, temos 8 setores circulares (que quando devidamente cortados são iguais!). Assim, cada um destes setores circulares representa 12,5% da área da pizza, uma vez que dividimos os 100% totais em 8 pedaços.
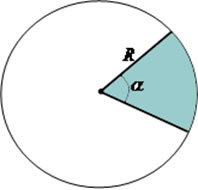
Porém, nem sempre pensar em relação ao total é interessante, e para isso foi criada uma maneira direta para determinar a área da seção. Vamos observar o setor circular abaixo:

Não sabemos qual a área deste setor, mas podemos relacionar o seu ângulo com o ângulo de uma circunferência completa, utilizando uma regra de três simples.

Portanto, isolando a área do setor circular, temos que:

Sendo assim, é determinada a área do setor circular apenas em função de seu raio e seu comprimento de arco!
Por fim, temos a área de um segmento circular. Para isso, vamos utilizar o segmento circular da figura a seguir:
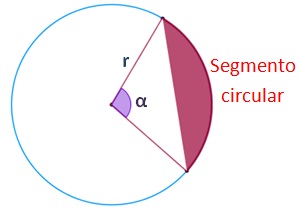
Como você já deve ter percebido, se trata de um segmento com as mesmas características do setor circular anterior, com raio r e ângulo . Porém, agora estamos interessados em apenas uma parcela deste setor, que será calculada através da diferença da área do setor e do triângulo formado. No entanto, existe uma maneira direta para se determinar a área do segmento circular, sem a necessidade de outras variáveis, através da seguinte equação:

Onde o ângulo deve ser utilizado em radianos! Com isso, demonstramos o cálculo de três figuras circulares planas, que são muito utilizadas em exercícios de geometria no Enem, portanto, é importante dedicar um tempo de estudo para estas equações, entendendo o seu funcionamento e unidades!