Já vimos em nosso portal um artigo relacionado à progressão aritmética (PA), podendo determinar sua razão, termo geral e também sua soma. No artigo de hoje, iremos conhecer mais sobre a progressão geométrica (PG) e também aprender a determinar seus termos gerais, somas, razões e produto.
Uma progressão geométrica é uma sequência de números (a1, a2, a3…an), em que a razão entre um número da sequência e seu número anterior possui o mesmo valor em toda a sua extensão. Este valor é conhecido como razão da PG e é representado pela letra q.
Consideremos a sequência (3,6,12,24,48,96, …). Assim, podemos observar que se trata de uma PG com razão q=2, pois:
![]()
A razão é fundamental para o entendimento da PG, visto que podemos descobrir os termos dela conhecendo apenas sua razão e o valor e posição de um de seus termos. Para isto, podemos utilizar a formulação do termo geral da PG, que é representado por:
an = a1 x qn-1
Onde an é o termo que ocupa a posição n na sequência, a1 é o termo inicial e q é a razão da PG. Note que podemos aplicar o termo geral em nossa sequência e determinar o sétimo termo, por exemplo:
a7 = a1 x q7-1
a7 = 3 x 26
a7 = 192
Também dependente da razão é a classificação da PG, que se dividem em 5 tipos principais, que são: crescente, quando q>1 e todos os termos da PG são positivos; decrescente, em que 0 < q < 1 com os termos positivos ou q>1 com os termos negativos; constante, quando q=1; singular, quando q=0 ou ainda oscilante, quando temos q<0. Resumindo:
| Tipo de PG | q |
|---|---|
| Crescente | >1, com os termos positivos |
| Decrescente | >1, com termos negativos ou 0<q<1 |
| Singular | 0 |
| Constante | 1 |
| Oscilante | <0 |
Podemos ainda obter a soma dos termos da progressão geométrica, para uma PG finita ou para uma infinita. Para uma sequência finita, em que seus termos variam da 1ª até a n-ésima posição, temos que:
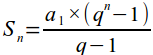
Com q≠1. Para o caso no qual q=1, iremos utilizar a seguinte equação:
Sn = n x an
Já para uma PG infinita, não podemos determinar o valor de n, assim as equações de soma anteriores não são válidas. Contudo, podemos utilizar outra equação para a sua soma, de maneira muito simples:
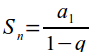
Para uma PG finita, podemos também calcular o produto de seus termos. O produto dos termos da PG pode ser escrito como:
![]()
Finalizando, no artigo de hoje podemos perceber que a progressão geométrica, embora seja um pouco mais complexa que a aritmética, ainda apresenta formulações simples e de fácil entendimento. Ademais, aprendemos a calcular sua razão, seu termo geral, classificá-la quanto a sua razão, determinar a sua soma e também calcular o seu produto.
Até a próxima.