Em nossos últimos artigos, estudamos o a definição e equações horárias do movimento retilíneo uniformemente variado (MRUV). Nesta postagem vamos explorar mais uma importante equação para o movimento uniformemente variado, a equação de Torricelli.
Antes de qualquer coisa vamos relembrar as equações para a velocidade e posição em um MRUV:
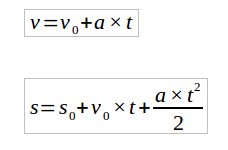
Analisando as duas equações, percebemos que tanto para a velocidade quanto para a posição, a referência é o tempo. Todavia, em muitos exercícios ou em aplicações práticas o valor do tempo não é conhecido, impedindo assim a utilização das equações anteriores. A equação desenvolvida por Torricelli consiste em isolar o tempo na equação da velocidade, substituindo-o na equação do movimento para o MRUV. Vamos então realizar este desenvolvimento:
Da equação da velocidade, isolando o tempo temos que:
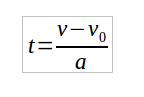
Substituindo na equação de movimento:
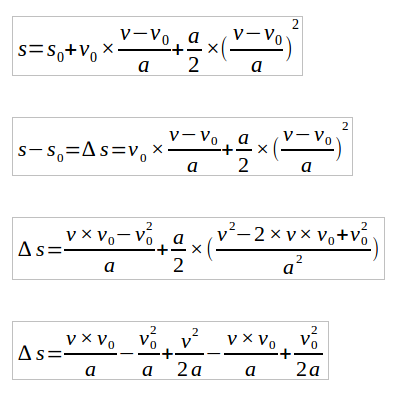
Reagrupando os termos que são iguais, então:
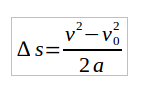
Isolando a velocidade final:
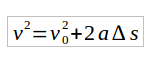
Esta é a equação de Torricelli. Note que, conforme havíamos citado anteriormente, esta equação não é dependente do tempo. A equação desenvolvida por Torricelli depende apenas da velocidade inicial do corpo, de sua aceleração e também da variação em seu deslocamento.
Muitas vezes a equação de Torricelli pode ser utilizada anteriormente às equações de velocidade e posição. Nestes casos, é possível determinar uma variável desconhecida pela equação de Torricelli e então substituir nas primeiras equações para encontrar a outra variável desejada.
Além disso, esta equação é fundamental para o estudo de queda livre e de lançamentos vertical e oblíquo, assuntos que veremos em sequência. Deste modo, devemos compreender corretamente a equação de Torricelli para que não fiquemos confusos nos próximos assuntos. Resolvendo alguns exercícios você rapidamente fixará todo o conteúdo e não terá dificuldade em explorar temas mais complexos. Então, vamos ao trabalho!


