Na postagem a seguir estudaremos um fenômeno presente em qualquer situação que envolve movimento: a resistência do ar. Vamos explicar como este fenômeno ocorre, exemplificando com situações do dia a dia, além de apresentar uma expressão para o seu cálculo.
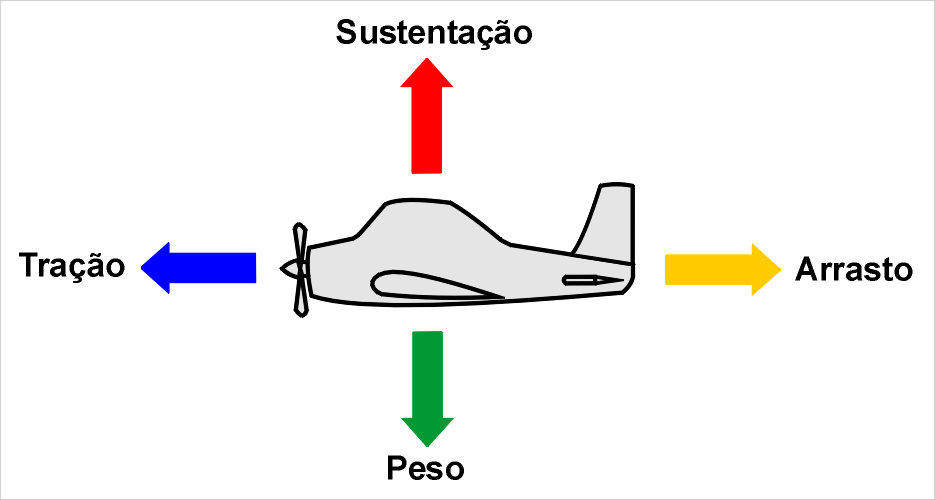
A força de resistência do ar, ou força de arrasto, está presente em todos os tipos de movimento, seja em maior ou menor intensidade. É caracterizada por ser uma força dissipativa, assim como a força de atrito, sendo exercida pelo meio em que o movimento ocorre (normalmente o ar). Abaixo está ilustrado um esquema simplificado de uma aeronave em voo, representando as forças atuantes em seu movimento:

Neste caso, assim como em veículos ou em qualquer prova que envolva velocidade o arrasto será prejudicial ao movimento, sendo minimizado ao máximo. No entanto existem algumas situações em que a força de arrasto é benéfica, como em saltos de paraquedas, o qual explicaremos adiante.
Antes disso, vamos a definição da força de arrasto. A força de resistência ao movimento é dada pela equação:
FR = k . v2
Onde v é a velocidade do objeto que está em movimento, utilizada em metros por segundo (m/s), e k é a constante de resistência ao movimento, expressa em Ns2/m2, e seus valores serão dependentes do formato do corpo, do meio em que o corpo se movimenta (geralmente é o ar, por isso comumente utilizamos “resistência do ar”) e principalmente da área de seção transversal do corpo, perpendicular ao movimento. Desta forma, percebemos que a orientação do objeto em movimento também é importante, e quando possível, devemos minimizar a área de seção que será perpendicular ao movimento.
Assim como mencionamos acima, a geometria do corpo também é de grande importância para a determinação de sua força de arrasto. Veja a seguir uma tabela contendo coeficientes de arrasto para algumas geometrias comuns:

Podemos observar a diferença no coeficiente de arrasto em função do posicionamento do corpo. Enquanto um cilindro posicionado “de frente” apresenta um coeficiente de arrasto igual a 0,82, o mesmo cilindro posicionado “de lado” apresenta um coeficiente igual a 1,15, devido a uma maior área de seção transversal.
Das formas demonstradas na tabela a que apresenta menor coeficiente de arrasto é o formato de gota. Reparando nos automóveis de alta performance, como carros esportivos e até mesmo os veículos de fórmula 1, as geometrias tendem para este formato, apresentando a menor resistência possível. É claro que os veículos não possuem exatamente este formato, por questões estéticas e também por outras questões relacionadas a aderência e estabilidade, mas se aproximam de um formato que permita uma menor resistência do meio.
Outro fato que devemos atentar é que a força de arrasto aumenta com o quadrado da velocidade, ou seja, se dobrarmos a velocidade, o arrasto aumentará em quatro vezes! Você pode perceber a presença da força de arrasto ao colocar a mão na janela de um veículo em movimento, e perceberá também que a medida que a velocidade aumenta, a força exercida sobre sua mão será maior!
Mas a força de arrasto nem sempre é prejudicial. Como falamos acima, é a força de arrasto que permite os saltos de paraquedas, uma vez que quando são abertos ocorre um aumento substancial na área em contato com o ar, equilibrando o paraquedista e fazendo com que o mesmo aterrisse em segurança!
Assim, podemos calcular os valores da força de arrasto em função da geometria que possuímos, assim como a nossa necessidade, seja ela de performance (minimizando o arrasto) ou de resistência (aumentando a resistência ao movimento)!


1 comment