Após abordar algumas definições e conceitos envolvendo principalmente as matrizes quadradas, vamos agora estudar as operações que envolvem a utilização de matrizes. Em nosso artigo de hoje, focaremos em duas operações principais: a determinação da transposta de uma matriz e a adição de matrizes.
Dada uma matriz qualquer do tipo Amxn definimos sua matriz transposta AT como sendo a matriz obtida pela troca ordenada de linhas por colunas, de modo que a matriz AT obtida seja do tipo nxm, como em nosso exemplo abaixo:
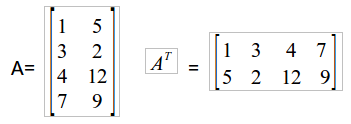
De uma maneira simplificada, podemos afirmar que para determinar uma matriz transposta, “o que é linha se torna coluna e o que é coluna se torna linha”. Note também que o cálculo da transposta de uma matriz não possui restrições quanto a sua dimensão, assim é possível determinar a transposta de matrizes quadradas e de matrizes não quadradas.
Para a adição de matrizes, iremos considerar duas matrizes A e B do tipo mxn. A adição dessas duas matrizes ocorrerá através da soma de seus termos em posições equivalentes e resultará em outra matriz, que trataremos como a matriz Cmxn em nosso seguinte exemplo:
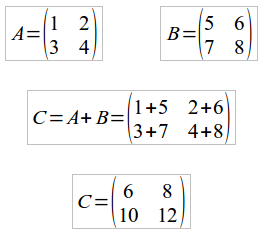
Assim como na determinação da transposta, não existem restrições quanto as dimensões das matrizes na hora de somá-las. O único ponto que deve ser salientado é que as matrizes devem possuir dimensões iguais, ou seja, não é possível somar uma matriz de ordem 3 com uma de ordem 4!
Dentro da adição de matrizes, devemos destacar quatro propriedades: A comutativa, a associativa, a do elemento oposto e a do elemento neutro:
- Comutativa: A propriedade comutativa indica que não há restrições quanto a ordem das somas, ou seja, A+B=B+A.
- Associativa: A propriedade associativa demonstra para três matrizes quaisquer que a sua soma não depende da ordem em que ocorre, ou seja, A+(B+C)= (A+B)+C.
- Elemento oposto: Dada uma matriz A, definimos a matriz oposta de A como sendo a matriz com o mesmo valor modular, porém com todos os sinais invertidos. O elemento oposto nos traz que a soma de uma matriz com a sua matriz oposta é igual a 0, ou seja, A+(-A)=(-A)+A=0.
- Elemento neutro: O elemento neutro nos indica que a soma de uma matriz qualquer com a matriz nula resulta nela mesma, ou seja, A+0=0+A=A.
Além do mais, podemos definir também a subtração entre matrizes. Dada duas matrizes de mesma ordem A e B, a subtração entre elas A-B é feita através da soma da matriz A com a oposta de B, como ilustrado em nosso exemplo:
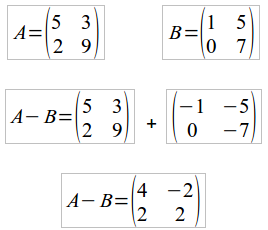
Após a conclusão destas operações, nos resta agora o estudo das multiplicações que envolvem as matrizes, que será estudado em nosso próximo artigo, aguarde!