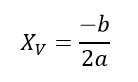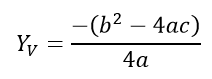Máximo (ou mínimo) de uma função quadrática

Em nossa postagem de hoje vamos falar sobre um assunto muito importante para as questões de matemática no Enem, que são os valores máximos (ou mínimos) de uma função quadrática. Para isso, vamos apresentar os cálculos necessários para obter estes valores extremos, assim como distinguir se o ponto será máximo ou mínimo. No final da postagem, apresentaremos também uma questão retirada do próprio Enem, para que você compreenda como este conteúdo pode ser abordado durante o Exame.

Máximo ou mínimo?

Para determinar se o ponto extremo da parábola (ou vértice) será máximo ou mínimo, devemos avaliar a concavidade desta parábola. Para isso, vamos considerar uma equação do segundo grau do formato

ax² + bx + c =0

Para este modelo de equação quadrática, a concavidade da parábola será definida pelo termo que acompanha o valor quadrado da função (a). Assim, teremos duas situações:

• a>0: Para as situações em que a>0, a concavidade da função estará voltada para cima, e o ponto extremo será o mínimo da função.
• a<0: Já para as situações em que a<0, a concavidade da função estará voltada para baixo, e o ponto extremo será o máximo da função

Depois de entendermos qual será o ponto da função e as situações em que estes pontos ocorrerão, é hora de aprendermos a calcular estes pontos.

Como determinar os pontos de máximo ou mínimo da função?

Uma vez que estamos trabalhando com figuras bidimensionais (os gráficos possuem coordenadas em x e y), deveremos determinar duas coordenadas para definir o máximo ou mínimo de uma função. Sendo assim, utilizaremos o mesmo modelo de função que apresentamos no começo deste artigo. Para este modelo de função, a coordenada x do ponto de máximo/mínimo será dado pela equação:

Já a coordenada no eixo y desta função será dada pela equação:

Questão do Enem

Com o objetivo de ilustrar como este conteúdo pode ser cobrado durante as provas do Enem, vamos apresentar a seguir um exercício retirado da primeira prova do Enem 2020 (aplicação regular), que aborda o conteúdo estudado nesta postagem.

“Uma empresa de chocolates consultou o gerente de produção e verificou que existem cinco tipos diferentes de barras de chocolate que podem ser produzidas, com os seguintes preços no mercado:

• Barra I: R$ 2,00;
• Barra II: R$ 3,50;
• Barra III: R$ 4,00;
• Barra IV: R$ 7,00;
• Barra V: R$ 8,00.

Analisando as tendências do mercado, que incluem a quantidade vendida e a procura pelos consumidores, o gerente de vendas da empresa verificou que o lucro L com a venda de barras de chocolate é expresso pela função L(x) = – x² + 14x – 45, em que x representa o preço da barra de chocolate.

A empresa decide investir na fabricação da barra de chocolate cujo preço praticado no mercado renderá o maior lucro.

Nessas condições, a empresa deverá investir na produção da barra”

a) I

b) II

c) III

d) IV

e) V

Alternativa correta: D.

Acesse o portal InfoEnem e tenha acesso aos melhores conteúdos e informações sobre o Enem 2021!