Já vimos em artigos anteriores os diferentes tipos de triângulos (clique aqui e veja o artigo), classificados segundo seu ângulo interno ou conforme a medida relativa entre os seus lados.
Dentre estes triângulos citados anteriormente, em nosso artigo de hoje, focaremos no triângulo retângulo, que será utilizado para explicarmos o conhecidíssimo (e importantíssimo!) teorema de Pitágoras.
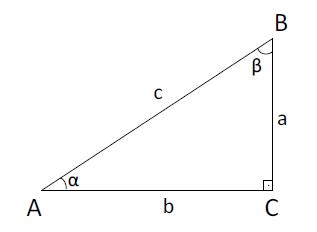
Como já observamos em um triângulo retângulo, os lados que formam o ângulo reto são denominados catetos e o lado que se opõe a este ângulo recebe o nome de hipotenusa. O teorema de Pitágoras diz que a soma do quadrado dos catetos é igual ao quadrado da hipotenusa. Para um triângulo retângulo qualquer temos:

c2=a2+b2
O teorema de Pitágoras é extremamente simples, mas também possui uma importância enorme! Certamente você irá utilizar o teorema de Pitágoras durante a sua prova, seja aplicando diretamente ou utilizando alguma aplicação sua, a qual veremos algumas em sequência.
Embora a maioria de vocês deva saber qual o valor da diagonal de um quadrado, também podemos obtê-la através do teorema de Pitágoras. Para isso, devemos apenas notar que a diagonal de um quadrado o divide em dois triângulos retângulos de lado L. feito isso devemos aplicar o teorema:

d2=L2+L2
d2=2L2
d=L√2
Podemos utilizar o teorema de Pitágoras para encontrar o valor da diagonal de um cubo. Devemos perceber que para o triângulo que utilizaremos o seu cateto que esta sobre a base do cubo é igual a sua diagonal, cujo valor calculamos acima:

D2=d2+a2
D2=(a√2)2+a2
D2=3a2
D=a√3
O teorema de Pitágoras também pode ser utilizado para a determinação da altura do triângulo equilátero. Para isso, vamos traçar a altura do triângulo, dividindo o mesmo em dois triângulos retângulos, podendo então aplicar o teorema de Pitágoras:

L2=H2+(L/2)2
L2=H2+L2/4
H2=L2-L2/4
H2=3L2/4
H=(L√3)/2
Como pudemos observar em nosso artigo de hoje, o teorema de Pitágoras é muito simples, porém fundamentalmente importante para os estudos e preparação para o Enem e outros vestibulares. Com ele podemos obter relações provenientes de triângulos retângulos e que nem sempre são demonstradas dessa forma. Exercitando esse assunto poderemos rapidamente entendê-lo e aplicá-lo. Portanto, vamos ao trabalho!