Utilizando a Fórmula de Bhaskara no Enem 2020

Em nossa postagem de hoje vamos estudar sobre um dos assuntos mais conhecidos e utilizados da matemática: a fórmula de Bhaskara. Para apresentar este conteúdo, que é muito abordado nas provas do Enem e também nos demais vestibulares, vamos apresentar as fórmulas utilizadas para este método, assim como algumas dicas para a resolução dos problemas. No final da postagem, vamos apresentar também uma questão retirada do próprio Enem que aborda o conteúdo apresentado.

A fórmula de Bhaskara

A fórmula de Bhaskara é o recurso mais utilizado para a resolução de equações do segundo grau. Apesar de existirem outros métodos que também resolvem com eficiência estas equações (como soma e produto, por exemplo), a fórmula de Bhaskara é bastante segura para resolver os problemas, chegando com facilidade ao resultado final. Para utilizar a fórmula de Bhaskara, devemos modelar a equação da seguinte maneira:

ax² + bx + c = 0

E destacamos que a utilização deste modelo é fundamental para a resolução do problema! Isso porque as fórmulas que utilizaremos para a resolução deste modelo de equação são funções dos termos a, b e c. Assim, se não formatarmos a equação corretamente, não conseguiremos resolvê-la. No entanto, modelar a equação neste formato é tarefa simples e você não encontrará dificuldades para realizar este passo! Com a equação neste formato, é hora de calcular o delta da equação:

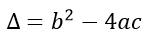
Ou seja, nosso delta é calculado em função dos três coeficientes da equação, o que demonstra novamente a importância da organização dos termos. Sobre os valores do delta, podemos ter três situações diferentes:

• Delta maior que zero: A equação possuirá duas raízes reais e distintas.
• Delta igual a zero: A equação apresentará duas raízes reais e iguais.
• Delta menor que zero: A equação não apresentará raízes reais.

Calculado o delta da equação, podemos partir para o cálculo das raízes (x₁ e x₂), que serão feitos em função dos coeficientes e do delta da equação.

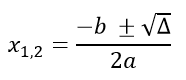
Com isso, é possível obter as duas raízes das equações do segundo grau, utilizando esta fórmula de maneira rápida e fácil. Destacamos também o cuidado com o sinal dos coeficientes, que farão total diferença durante a resolução das equações.

Questão do Enem

Como mencionamos no início da postagem, a fórmula de Bhaskara é utilizada em diversos exercícios do Enem, seja para a resolução direta do problema ou como parte da solução. Para demonstrar como este conteúdo pode ser abordado durante o exame, vamos apresentar a seguir uma questão retirada da prova de 2013 do Enem, em que podemos utilizar a fórmula de Bhaskara para resolver diretamente o exercício. Confira!

“A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante do desligamento (t = 0) e varia de acordo com a expressão (t em minutos):

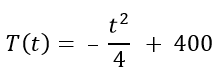
Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge temperatura de 39 °C. Qual o tempo mínimo de espera, em minutos, após desligar o forno, para que a porta possa ser aberta?”

a) 19,0

b) 19,8

c) 20,0

d) 38,0

e) 39,0

Alternativa correta: d.

Acesse o portal InfoEnem e tenha acesso aos melhores conteúdos e informações sobre o Enem 2020!